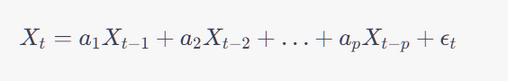The concept of "poles" in the context of Maximum Entropy Method (MEM) forecasting and power spectrum analysis is fundamentally tied to the order of the autoregressive (AR) model employed in the method. The poles are essentially the roots of the characteristic equation of the AR process, and they play a crucial role in defining the behavior and properties of the system.
In MEM, a time series is modeled as an autoregressive process of a certain order. The order of the AR model (denoted as 'p') is equivalent to the number of poles in the system. This means that if we have an AR(p) model, there are 'p' poles or previous values of the series that are used to predict the next value in the series. Mathematically, this can be expressed as:
where Xt is the value at time 't', α1, α2,...,αp are the coefficients of the AR model, and εt is white noise.
The poles of the AR model are important because they determine the characteristics of the time series, such as its cyclical behavior and its memory. In terms of the power spectrum, the poles correspond to peaks in the spectrum, indicating frequencies at which the time series has significant power.
The choice of the number of poles (or the AR order) is critical in MEM analysis. A higher number of poles allows the model to capture more complex patterns in the data, potentially leading to more accurate forecasts and a more detailed power spectrum. However, using too many poles can result in overfitting, where the model becomes too tailored to the historical data and may not generalize well to future data.
In practice, the choice of the number of poles is a trade-off between resolution and stability, and it often depends on the characteristics of the time series and the goals of the analysis. Some guidelines and criteria, such as the Akaike Information Criterion (AIC) or the Bayesian Information Criterion (BIC), can be used to select an optimal number of poles, but these would be difficult to implement in Pinescript.
In general, we have found that a Poles value that is 40% of the Window Size yields good and stable results and that is the value we use if Poles is set to 0. You can experiment with customizing the Poles value but you should probably stay within a range of 20% to 80% of the Window Size or you will risk underfitting/overfitting the data. And, regardless, Poles must always be in the range of 1 to Window Size - 1.
See Also: